 •
9:00 a.m. 8 Tháng 4, 2024
•
1
•
9:00 a.m. 8 Tháng 4, 2024
•
1
Summary LQDOJ Contest #9
LQDOJ Contest #9 đã được diễn ra vào ngày \(07/04/2024\) từ \(19:30\) đến \(22:00\) cùng ngày một cách tốt đẹp. Trong suốt \(2\) giờ \(30\) phút diễn ra contest đã có tổng cộng \(x\) lượt nộp bài, trong đó có \(x\) lượt AC. Đó thực sự là những con số ấn tượng, cũng như cho thấy kì thi đã diễn ra một cách suôn sẻ. Thay mặt cho toàn bộ Team Shiba nói riêng cũng như LQDOJ nói chung, mình xin cảm ơn tất cả các bạn đã nhấp vào nút "Tham gia" contest. Solution của các bài cùng rating sẽ được công bố trong thời gian gần nhất, còn bây giờ hãy cùng mình xem lại kết quả contest qua nhé!
Kết Quả
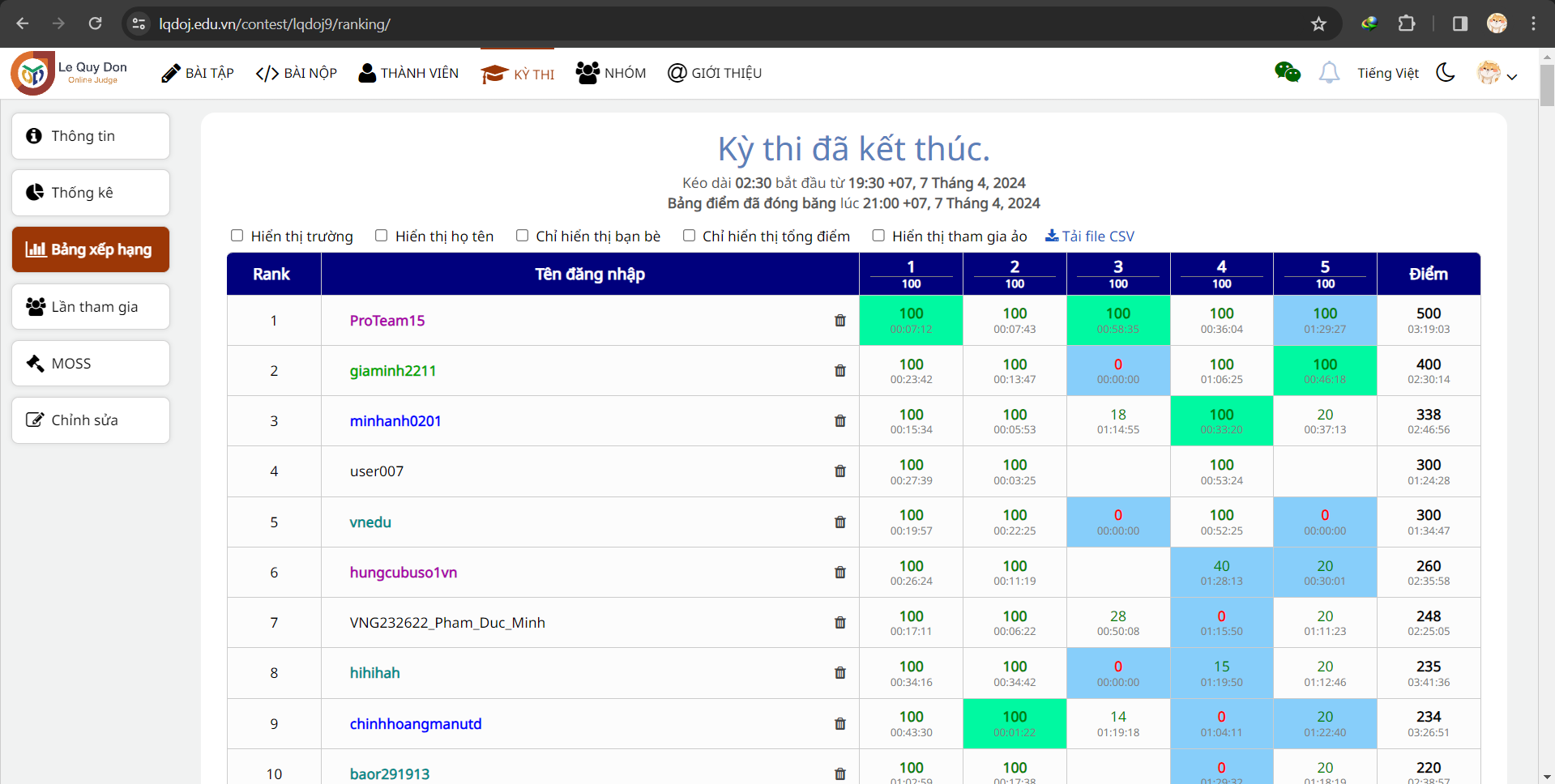
Đây là bảng xếp hạng trước khi phá băng.
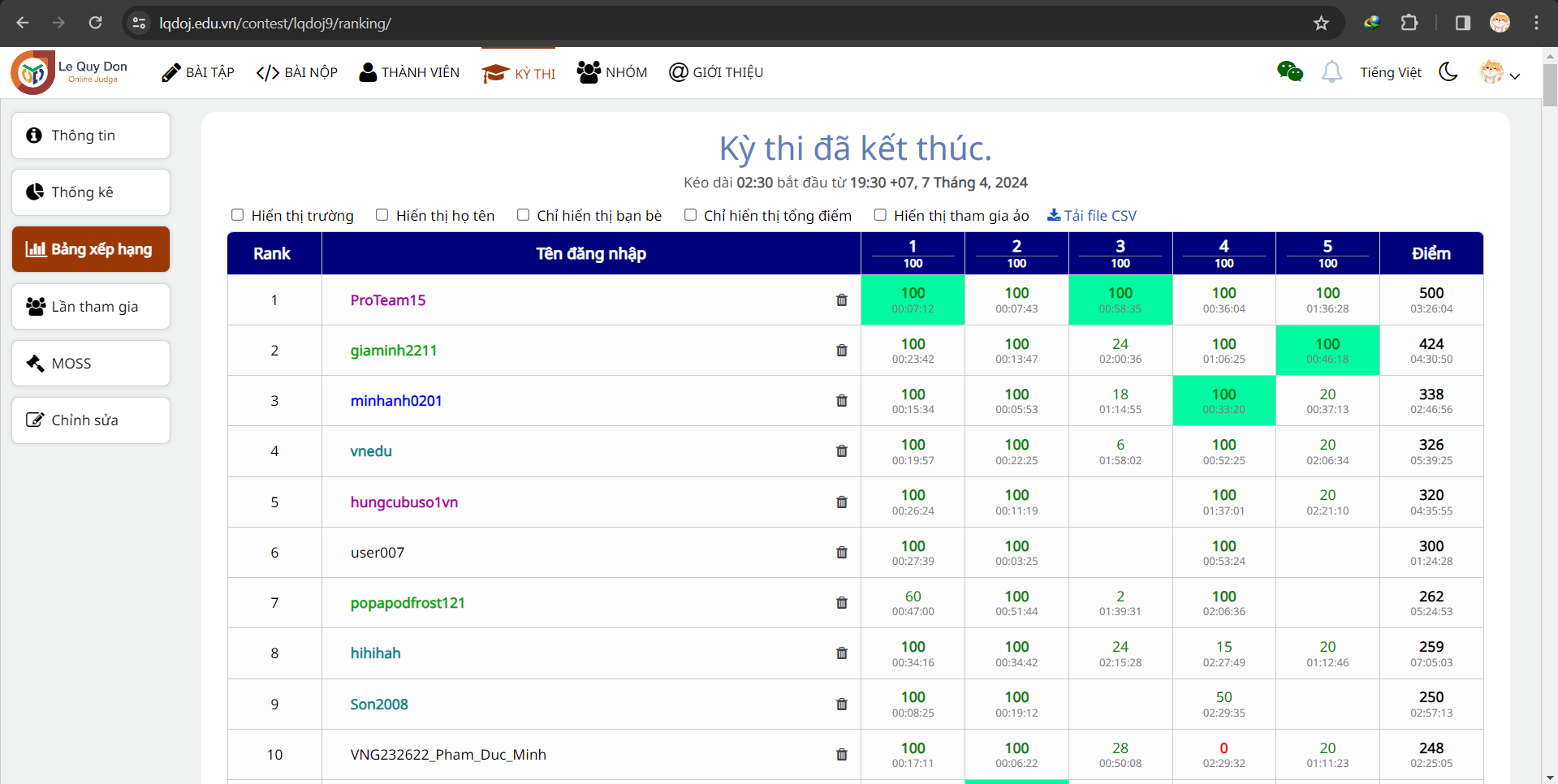
Và đây là bảng xếp hạng chính thức sau khi phá băng và kiểm tra gian lận.
Kết quả chính thức của LQDOJ Contest #9 có thể được tìm thấy tại đây. Phía trên là ảnh chụp màn hình của những vị trí đầu tiên trong contest trên.
Chúng mình xin được chúc mừng các bạn First AC các bài:
-
First AC bài \(1\):
-
First AC bài \(2\):
-
First AC bài \(3\):
-
First AC bài \(4\):
-
First AC bài \(5\):
Và chúng mình xin chúc mừng thí sinh đã đạt được top \(1\) và là thí sinh duy nhất AC cả \(5\) bài.
Gian Lận
LQDOJ Contest 9 đợt này Team Shiba chúng mình phát hiện các trường hợp gian lận sau:
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và
-
và Y2JNguyenDucHieu
-
và Y2JNguyenDucHieu
-
và
-
và
-
và
-
và
-
và
-
và
-
và
Toàn bộ bằng chứng gian lận chúng mình xin được công bố tại đây. Các bạn có quyền khiếu nại với BTC về hành vi của mình trước \(22:00\) ngày \(10/04/2024\) bằng cách liên hệ với BTC theo thông tin ở dưới. Chúng mình sẽ thu hồi vĩnh viền tài khoản LQDOJ của các bạn nếu các bạn không liên hệ lại với BTC!
Rate
Chúng mình sẽ rate contest muộn nhất trước \(23:59\) ngày \(11/04/2024\) :Đ
Liên hệ với Ban Tổ Chức
-
Fanpage: LQDOJ
-
Admin: Nguyễn Đức Thuận -
 •
8:00 p.m. 5 Tháng 4, 2024
•
1
•
8:00 p.m. 5 Tháng 4, 2024
•
1
LQDOJ Contest #9
Xin chào các bạn!
Đã \(2\) tháng chúng ta chưa được gặp nhau rồi nhỉ? Chúng mình đã trở lại sau một thời gian dài vắng bóng rồi đây. Chúng mình đã được sự cho phép của và tổ chức LQDOJ Contest 9 nhằm giúp các bạn có một sân chơi bổ ích sau kì thi Olympic Miền Trung Tây Nguyên và tạo cơ hội cho các bạn có thể tăng điểm rating đổi màu :Đ
Thông tin và thể lệ của kì thi cơ bản vẫn sẽ như các lần trước:
-
Số lượng bài: Gồm \(5\) bài được được sắp xếp lộn xộn (ngẫu nhiên).
-
Thời gian làm bài: \(150\) phút (\(2\) tiếng \(30\) phút) tính từ \(19:30\) ngày \(07\)/\(04\)/\(2024\) (Chủ Nhật).
-
Thể lệ cơ bản vẫn như mọi lần chúng mình tổ chức các contest bình thường, cụ thể là như sau:
- Tất cả các bài đều được chấm với đầy đủ bộ test ngay trong kì thi.
- Các thí sinh được xếp hạng theo tổng điểm. Các thí sinh bằng điểm nhau sẽ được xếp hạng bằng tổng thời gian của của mỗi bài tập các bạn có nộp.
- Bảng xếp hạng sẽ bị đóng băng trong \(60\) phút cuối của contest để tăng độ kịch tính.
- Bảng xếp hạng sẽ được ẩn ngay sau khi contest kết thúc nhằm phục vụ công tác kiểm tra gian lận.
- Điểm của bài sẽ là tổng điểm của các bài, điểm của bài là điểm cao nhất trong các lần nộp của bài đó.
Contest này được rating cho tất cả các bạn tham gia kì thi. Vì vậy các bạn hãy tham gia vào contest này để có cơ hội đổi màu các bạn nhé :Đ
Các bạn hãy theo dõi Fanpage LQDOJ tại đây để không bỏ lỡ thông tin về contest nha.
Mirror Bán kết OLP MTTN 2024
Chào các bạn,
Nhằm tạo điều kiện cho các bạn chưa được vào Bán kết OLP MTTN có thể trải nghiệm các Contest của vòng thi bán kết, LQDOJ phối hợp cùng BTC OLP MTTN 2024 tổ chức Kỳ thi Mirror cho các bảng thi để các bạn có thể tham gia thi đấu giao lưu. Kỳ thi sẽ được tính ratìng cho các bạn tham gia.
Thời gian thi: Từ 14h00 đến 17h00 ngày 09/03/2024.
Bảng Không chuyên tính rating cho các bạn có rating bé hơn 1700, đường dẫn tại đây:
Bảng Chuyên tin tính rating cho tất cả các bạn, đường dẫn thi tại đây:
Chúc các bạn làm bài vui vẻ!
 •
11:00 a.m. 8 Tháng 2, 2024
•
0
•
11:00 a.m. 8 Tháng 2, 2024
•
0
Summary LQDOJ Contest #8
LQDOJ Contest #8 - Tạm biệt năm Quý Mão đã diễn ra vào ngày \(07/02/2024\) dương lịch từ \(19:08\) đến \(21:38\) một cách tốt đẹp và không có sai sót về bộ đề cũng như bộ test. Contest này đánh dấu cột mốc một năm Team Shiba chúng mình đã đồng hành cùng LQDOJ và các bạn tổ chức những contest hay. Với tổng cộng \(1883\) bài nộp, các bạn đã thể hiện sự cố gắng hết mình trong contest, chúng mình thực sự rất vui vì điều đó. Thay mặt cho Team Shiba nói riêng và LQDOJ nói chung, mình xin cảm ơn \(202\) người tham gia contest vào tối hôm qua. Bây giờ hãy xem bảng rank chính thức của contest nhé :Đ
Kết Quả
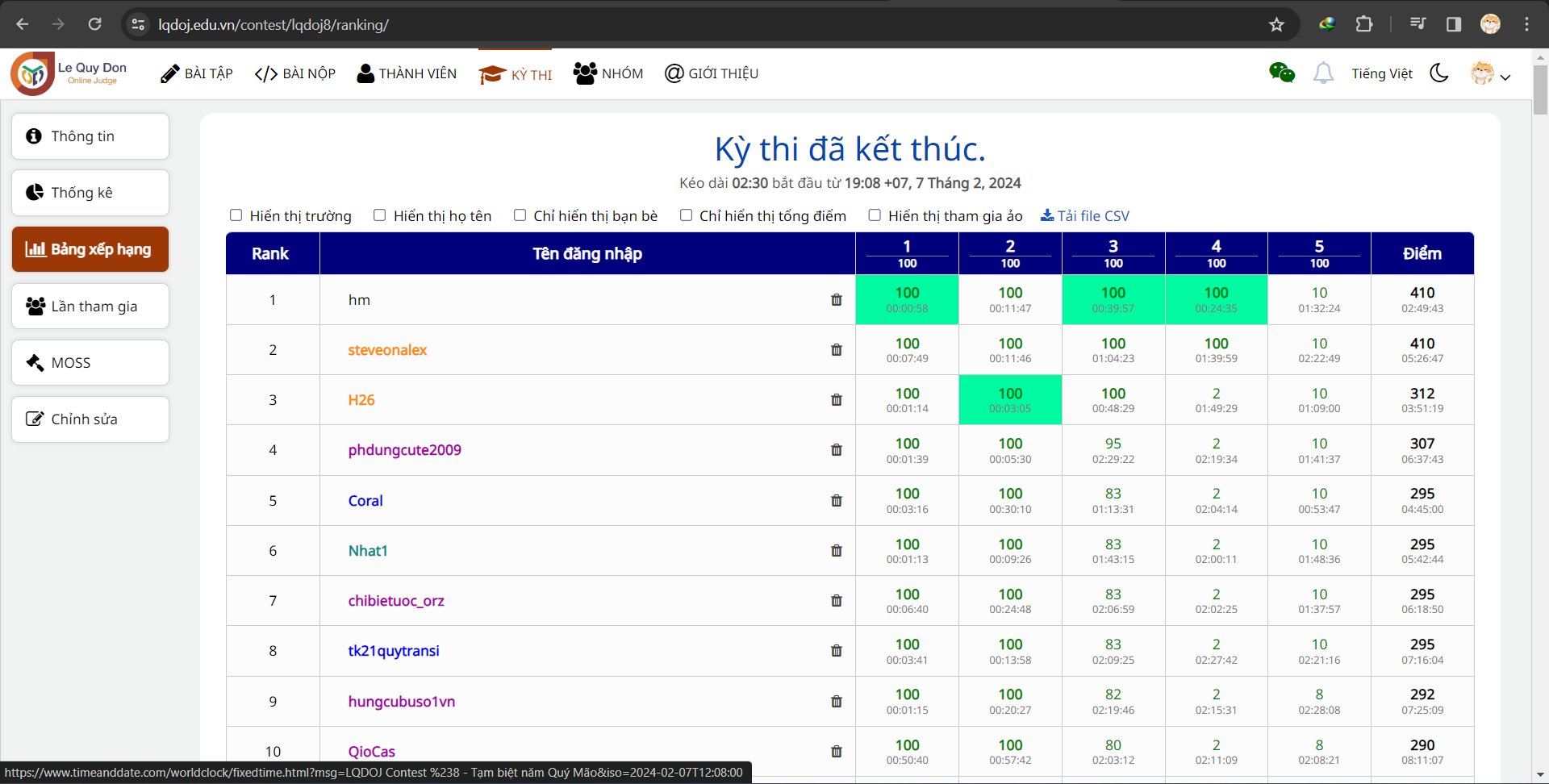
Kết quả chính thức của LQDOJ Contest #8 có thể được tìm thấy tại đây. Phía trên là ảnh chụp màn hình của những vị trí đầu tiên trong contest trên.
Giải Thưởng
Chúng mình xin được gửi lời chúc mừng tới những bạn sau đây đã nhận được lì xì tết của LQDOJ:
-
Top \(1\) (\(333.000\) VNĐ):
-
Top \(2\) (\(222.000\) VNĐ):
-
Top \(3\) (\(111.000\) VNĐ):
-
First AC bài \(1\) (\(11.000\) VNĐ):
-
First AC bài \(2\) (\(22.000\) VNĐ):
-
First AC bài \(3\) (\(33.000\) VNĐ):
-
First AC bài \(4\) (\(44.000\) VNĐ):
-
First AC bài \(5\) (\(55.000\) VNĐ): Không có ai AC bài này nên sẽ không có giải First AC cho bài \(5\).
Trao Giải
chúng mình xin chúc mừng các bạn đã đạt được giải thưởng! Để nhận giải thưởng của mình, các bạn vui lòng liên hệ lại với GS. - Nguyễn Đức Thuận qua Facebook Nguyễn Đức Thuận (floweronstone)
Gian Lận
LQDOJ Contest #8 đợt này Team Shiba chúng mình phát hiện hai trường hợp gian lận sau:
Toàn bộ bằng chứng chúng mình đã công bố ở trên, và xét thấy bài làm gian lận thì chúng mình sẽ không nhận kháng cáo (không nhận trường hợp tài khoản phụ nộp qua tài khoản chính vì hành vi đó cũng tính là vi phạm). Xin lưu ý!
Liên hệ với Ban Tổ Chức
-
Fanpage: LQDOJ
-
Admin: Nguyễn Đức Thuận -