3. LQDOJ Cup 2023 - Round 1 - Wireless
Công ty viễn thông Sunchain (trực thuộc tập đoàn Edison chuyên sản xuất xe máy điện) đang thử nghiệm công nghệ mạng không dây mới.
Mạng lưới thử nghiệm hiện tại gồm \(n\) trạm phát sóng, được kết nối với nhau thông qua \(n - 1\) đường dây mạng. Đường dây thứ \(i\) kết nối giữa trạm \(u_{i}\) và \(v_{i}\), và có chiều dài là \(w_{i}\) mét. Việc kết nối các trạm đảm bảo thông tin luôn được truyền tải giữa hai trạm phát sóng bất kỳ.
Mỗi trạm phát sóng sẽ hoạt động ở một trong hai trạng thái: chế độ hoạt động (vừa phát tín hiệu mới, vừa nhận thông tin hoặc trung chuyển truyền tin từ trạm này sang trạm khác), hoặc chế độ nghỉ ngơi (chỉ nhận thông tin hoặc trung chuyển truyền tin). Khi phát một tín hiệu từ trạm \(s\) gửi tới trạm \(t\) bất kỳ, chi phí truyền tin sẽ bằng tổng độ dài của các đường dây mạng trên đường đi đơn duy nhất đi từ \(s\) đến \(t\).
Các kỹ sư có kế hoạch thử nghiệm sơ bộ \(q\) lần. Vì đang trong quá trình thử nghiệm, đôi khi các kỹ sư của Sunchain sẽ cho một số trạm nghỉ ngơi. Ở lần thử nghiệm thứ \(i\), các kỹ sư sẽ bật \(k_{i}\) trạm phát sóng \(s_{1}, s_{2}, \ldots, s_{k_{i}}\) ở chế độ hoạt động, và các trạm còn lại được cho nghỉ ngơi.
Cơ chế thử nghiệm tương đối đơn giản: Chọn ra một trạm phát sóng tiếp nhận \(T_{i}\) (có thể hoạt động hoặc là nghỉ ngơi) để thu thập dữ liệu. Tất cả \(k_{i}\) trạm này sẽ cùng nhau phát tín hiệu gửi tới trạm \(T_{i}\), và chi phí cho việc thử nghiệm này bằng tổng chi phí truyền tin của từng trạm hoạt động tới trạm tiếp nhận \(T_{i}\).
Sunchain đang trong giai đoạn khó khăn, nên việc thử nghiệm cũng cần phải tiết kiệm.
Yêu cầu: với mỗi lần thử nghiệm sơ bộ, bạn hãy chọn ra trạm tiếp nhận sao cho chi phí thử nghiệm là thấp nhất nhé!
Input
- Dòng đầu tiên lần lượt gồm hai số nguyên dương \(n\) và \(q\) \((1 \leq n \leq 5 \times 10^{5}, 1 \leq q \leq 10^{5})\) là số trạm phát sóng và số thử nghiệm.
- \(n - 1\) dòng tiếp theo, dòng thứ \(i\) lần lượt gồm ba số \(u_{i}, v_{i}, w_{i}\) \((1 \leq u_{i}, v_{i} \leq n, u_{i} \neq v_{i}, 1 \leq w_{i} \leq 10^{6})\) thể hiện một đường dây kết nối giữa trạm \(u_{i}\) và \(v_{i}\) có chiều dài là \(w_{i}\) mét.
- \(q\) dòng tiếp theo, dòng thứ \(j\) bắt đầu bằng số nguyên dương \(k_{j}\), kế đến là \(k_{j}\) số phân biệt \(s_{1}, s_{2}, \ldots, s_{k_{j}}\) \((1 \leq k_{j} \leq n, 1 \leq s_{i} \leq n)\), thể hiện một lần thử nghiệm.
- Dữ liệu đảm bảo \(\sum_{j = 1}^{q} k_{j} \leq 5 \times 10^{5}\).
Output
- In ra \(q\) dòng, dòng thứ \(j\) chứa duy nhất một số \(c_{j}\), cho biết chi phí tối thiểu trong lần thử nghiệm sơ bộ thứ \(j\).
Scoring
- Subtask \(1\) (\(20\%\) số điểm): \(n, q \leq 500\).
- Subtask \(2\) (\(20\%\) số điểm): \(k_{j} = 2\).
- Subtask \(3\) (\(20\%\) số điểm): \(k_{j} = 3\).
- Subtask \(4\) (\(20\%\) số điểm): \(q = 1\).
- Subtask \(5\) (\(20\%\) số điểm): Không có ràng buộc gì thêm.
Example
Test 1
Input
8 3
1 2 2
1 3 3
2 4 4
3 5 3
3 6 5
6 7 1
6 8 6
2 2 8
3 4 7 8
4 1 5 7 8Output
16
21
23Note
Dưới đây là hình vẽ thể hiện mạng lưới các trạm phát sóng:
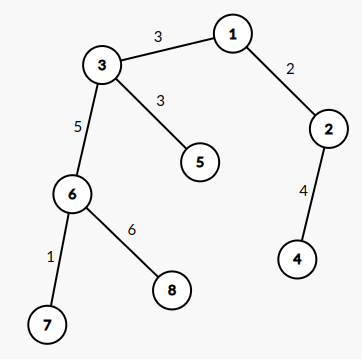
Gọi \(d(u, v)\) là khoảng cách giữa hai trạm phát sóng \(u\) và \(v\).
- Trong thử nghiệm đầu tiên, ta chọn trạm \(2\) làm trạm phát sóng tiếp nhận, tổng chi phí là \(d(2, 2) + d(2, 8) = 0 + 16 = 16\).
- Trong thử nghiệm thứ hai, ta chọn trạm \(6\) làm trạm phát sóng tiếp nhận, tổng chi phí là \(d(6, 4) + d(6, 7) + d(6, 8) = 14 + 1 + 6 = 21\).
- Trong thử nghiệm thứ ba, ta chọn trạm \(3\) làm trạm phát sóng tiếp nhận, tổng chi phí là \(d(3, 1) + d(3, 5) + d(3, 7) + d(3, 8) = 3 + 3 + 6 + 11 = 23\).