Sau khi rủ được cô "bạn gái cũ" kia đi chơi thành công, hai người đã có một khoảng thời gian cực kì vui vẻ ở bên nhau, dẫu cho biết rằng shiba vẫn đau khổ vì lụy tình. Trong quãng thời gian du lịch đó, "bạn gái cũ" của shiba đã đưa ra một bài toán mà shiba đã từng không làm được khi cô ấy hỏi để thách đố và sẽ cưới _minhduc nếu cậu ấy trả lời được...

Bài toán đó như sau:

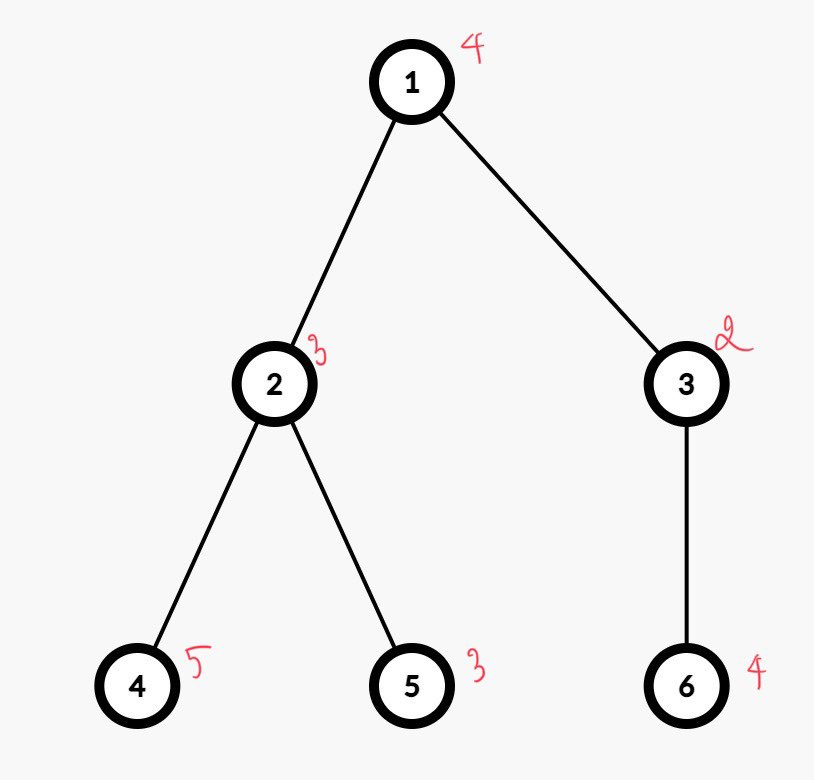
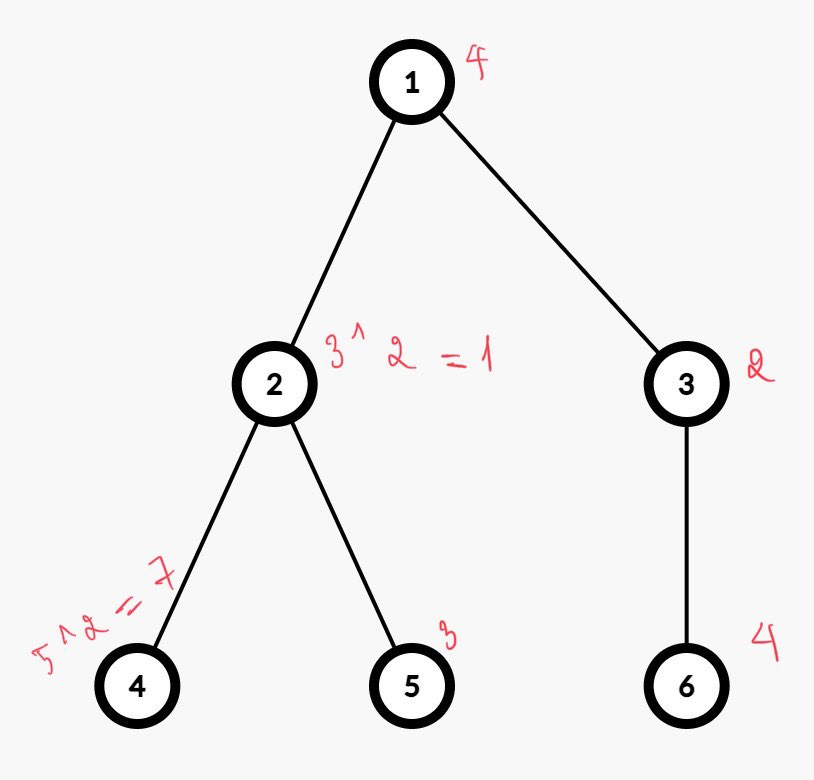
Bạn được cho một cây có \(n\) đỉnh và \(n-1\) cạnh và một mảng \(a\) gồm \(n\) phần tử. Ban đầu giá trị của đỉnh thứ \(i\) bằng \(a_i\). Có hai loại truy vấn:

• 1 u v p: Gọi \(s_1, s_2,..., s_k\) là các đỉnh trên đường đi từ \(u\) đến \(v\). Sau đó thực hiện thao tác \(\oplus\) với tất cả các đỉnh đó, nói cách khác ta gán cho \(a_{s_1} = a_{s_1} \oplus p\), \(a_{s_2} = a_{s_2} \oplus p\),..., \(a_{s_k} = a_{s_k} \oplus p\) \((0 \le p \le 2^{10}-1)\).
• 2 u v: Gọi \(s_1, s_2,..., s_k\) là các đỉnh trên đường đi từ \(u\) đến \(v\). Sau đó cần đưa ra tổng trọng số đỉnh của các nút trên đường đi từ \(u\) đến \(v\), nói cách khác cần đưa ra tổng \(S = a_{s_1} + a_{s_2} + ... + a_{s_k}\).

Do bài toán quá khó, _minhduc lại phải nhờ tới quân sư của mình - quân sư của kẻ phản diện, đó là Flower_On_Stone. Tuy nhiên, Flower_On_Stone đang có chuyến công tác nước ngoài nên không giúp cậu ấy được. Lần này, cậu ấy quyết định sẽ đưa lên đây để hỏi các bạn. Các bạn hãy giúp cậu ấy nhé.

Biểu thức \(x\) \(\oplus\) \(y\) biểu diễn phép toán tử XOR của hai số \(x\) và \(y\).

Yêu cầu: Với mỗi truy vấn loại \(2\), đưa ra kết quả trên một dòng.

Tuy nhiên, chuyện đi chơi riêng tư này đã bị tai mắt của shiba biết được. Từ đây, mời bạn về LQDOJ Contest #6 - Bài 5 để hóng drama nhé :Đ.

Input

• Dòng đầu tiên chứa một số nguyên \(\phi\) - số thứ tự của subtask chứa test đó \((1 \le \phi \le 6)\).
• Dòng thứ hai chứa một số nguyên dương \(n\) (\(1 \le n \le 10^5\)).
• Dòng thứ ba chứa \(n\) số nguyên \(a_1,a_2,...a_n\) (\(1 \le a_i \le 2^{10}-1\)).
• \(n-1\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(u,v\) - mô tả một cạnh của cây.
• Dòng tiếp theo chứa một số nguyên dương \(q\) (\(q \le 10^5\)) - số lượng truy vấn.
• \(q\) dòng cuối cùng, mỗi dòng chứa một truy vấn như mô tả ở trên.

Output

• Với mỗi truy vấn loại \(2\), đưa ra kết quả bài toán trên một dòng.

Scoring

• Subtask \(1\) (\(15\%\) số điểm): \(n,q \le 100\).
• Subtask \(2\) (\(20\%\) số điểm): cây thoả mãn điều kiện với hai cạnh \((u,v)\) bất kì \((u < v)\) thì \(u = \lfloor \frac{v}{2} \rfloor\).
• Subtask \(3\) (\(20\%\) số điểm): mọi truy vấn update đều có \(u = v\).
• Subtask \(4\) (\(10\%\) số điểm): cây thoả mãn điều kiện đỉnh \(u\) được nối với đỉnh \(u+1\) với mọi \(1 \le u \le n-1\).
• Subtask \(5\) (\(15\%\) số điểm): cây thoả mãn điều kiện mỗi đỉnh không có nhiều hơn \(2\) cạnh.
• Subtask \(6\) (\(20\%\) số điểm): không có ràng buộc gì thêm.

Example

1
6
4 3 2 5 3 4
1 2
1 3
2 4
2 5
3 6
2
1 2 4 2
2 1 2

5