Các nhà khảo cổ vừa tìm thấy một siêu cân thăng bằng thời tiền sử. Cấu trúc của nó hoặc là chỉ bao gồm một móc treo tạ hoặc là gồm một thanh ngang độ dài nguyên dương, một dây treo chia thanh này thành hai cánh tay đòn có độ dài nguyên dương và mỗi đầu mút của thanh được treo một siêu cân thăng bằng. Các móc treo tạ sẽ được đánh số, việc đánh số các móc treo tạ cho một siêu cân được làm như sau:

• Nếu siêu cân chỉ bao gồm một móc treo tạ thì dùng số nguyên dương nhỏ nhất chưa dùng để đánh số cho móc treo này;
• Ngược lại, tiến hành đánh số các móc treo tạ cho siêu cân ở bên mút trái của thanh, sau đó đánh số các móc treo tạ cho siêu cân ở bên mút phải của thanh.

Khi treo các quả tạ có khối lượng nguyên dương vào các móc treo tạ, cân sẽ thăng bằng nếu với mọi thanh ngang, tỷ lệ giữa tổng khối lượng bên trái và tổng khối lượng bên phải bằng với tỷ lệ giữa độ dài cánh tay đòn bên phải và độ dài cánh tay đòn bên trái. Ta nói dãy nguyên dương \(a=(a_1,a_2,\ldots,\ a_k)\) là dãy cơ sở của một siêu cân nếu k bằng số móc treo tạ và khi treo các quả tạ vào các móc theo thứ tự thì siêu cân này thăng bằng, đồng thời tổng các số trong dãy a là nhỏ nhất có thể. Tổng các số trong dãy cơ sở của một siêu cân được gọi là số khối của siêu cân đó. Ví dụ siêu cân trong hình sau có cơ sở là \((2,3,5,3,1,1)\) và số khối là \(15\).

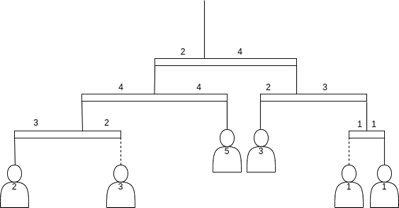
Dễ thấy mỗi siêu cân đều tồn tại và duy nhất một cơ sở. Giả sử \((a_1,a_2,\ldots,\ a_k)\) là cơ sơ của siêu cân ban đầu. Hiện tại có một số móc treo tạ đã bị hỏng. Việc phục chế là thay thế tất cả các móc treo tạ này, mỗi móc treo tạ được thay bằng một siêu cân có số khối tương đương với khối lượng quả tạ treo tại đó. Tức là nếu móc treo tạ thứ \(i\) bị hỏng, nó sẽ được thay thế bằng một siêu cân nào đó có số khối bằng \(a_i\). Các nhà khảo cổ đã thử nhiều cách phục chế khác nhau và ghi lại cơ sở của siêu cân sau phục chế.
Yêu cầu: Hãy đếm số dãy nguyên dương là cơ sở của ít nhất một siêu cân sau phục chế.

Input

Phần đầu của input mô tả cấu trúc của siêu cân đã cho. Cách mô tả cấu trúc của một siêu cân như sau:

• Chỉ gồm một số 0 nếu siêu cân là một móc treo tạ;
• Ngược lại sẽ gồm 3 phần:
  • Phần một gồm hai số nguyên dương L,R là độ dài cánh tay đòn bên trái và bên phải;
  • Phần hai mô tả cấu trúc của siêu cân được treo bên mút trái của thanh;
  • Phần ba mô tả cấu trúc của siêu cân được treo bên mút phải của thanh.

Phần sau của input mô tả các móc treo tạ bị hỏng, gồm một số nguyên dương \(m\) và \(m\) số nguyên dương phân biệt là chỉ số của các móc treo tạ đó.

Output

In ra một số nguyên là số dãy cơ sở khác nhau có thể có của siêu cân sau khi phục chế, do kết quả có thể rất lớn nên chỉ cần in ra phần dư khi chia cho \(({10}^9+7)\).

Scoring

• Subtask \(1\) (\(30\%\) số điểm): \(1\le m,\ L,\ R\le10\) và số thanh ngang không quá \(30\);
• Subtask \(2\) (\(40\%\) số điểm): \(1\le m,\ L,\ R\le10\) và số thanh ngang không quá \({10}^4\);
• Subtask \(3\) (\(30\%\) số điểm): \(1\le m,\ L,\ R\le30\) và số thanh ngang không quá \({10}^5\).

Example

2 4
4 4
3 2
0
0
0
2 3
0
1 1
0
0
2 2 5

3