Tìm hiểu văn hóa
Xem PDFTrong truyền thuyết thời xa xưa, Miền Trung - Tây Nguyên là một vùng đất rộng lớn với nguồn tài nguyên phong phú và ẩm thực đa dạng, đứng đầu bởi một vị vua anh minh. Tương truyền, các đơn vị số đo về khoảng cách, vận tốc, thời gian vào thời đó rất khác biệt, không cùng đơn vị đo lường như bây giờ.
Vùng đất này được tổ chức thành \(N\) thành phố và \(N-1\) cung đường hai chiều. Cung đường thứ \(i\) có độ dài \(w_i\) nối hai thành phố \(a_i\) và \(b_i\) với nhau, và các cung đường này được xây dựng để bảo đảm hai thành phố bất kỳ có thể đến được với nhau thông qua một hoặc nhiều cung đường khác nhau.
Là người ưa thích tìm tòi văn hoá các địa phương trong vương quốc của mình, đức vua đã triệu tập \(M\) cận vệ để đi khám phá. Người cận vệ thứ \(j\) \((1\le j\le M)\) được cấp một con chiến mã có thể chạy với vận tốc tối đa \(s_j\) (thời gian tăng tốc ban đầu không đáng kể). Anh ta sẽ xuất hành vào thời điểm \(t_j\) để đi từ thành phố \(u_j\) đến thành phố \(v_j\). Lưu ý rằng, thời điểm đặt chân lên một thành phố có thể là một số thực.
Yêu cầu: Cho biết \(Q\) thành phố, với mỗi thành phố, hãy cho biết thời điểm đầu tiên có một cận vệ của nhà vua đặt chân đến là khi nào.
Input
- Dòng đầu ghi ba số nguyên \(N, M\) và \(Q\) là số lượng thành phố, số người cận vệ và số thành phố được truy vấn.
- Dòng thứ \(i\) trong số \(N - 1\) dòng tiếp theo chứa \(3\) số nguyên \(a_i, b_i, w_i\) cho biết cung đường thứ \(i\) nối giữa hai thành phố \(a_i, b_i\) với độ dài \(w_i\).
- Dòng thứ \(j\) trong số \(M\) dòng tiếp theo chứa \(4\) số nguyên \(u_{j}, v_{j}, t_{j}, s_{j}\) cho biết tại thời điểm \(t_j\) người cận vệ thứ \(j\) sẽ lấy cỗ xe có tốc độ \(s_j\) để đi từ thành phố \(u_j\) đến \(v_j\).
- Dòng cuối cùng chứa \(Q\) số nguyên phân biệt \(k_1, k_2, \ldots, k_Q\) là số đỉnh mà đức vua quan tâm.
Output
- Ghi ra \(Q\) dòng, dòng thứ \(i\) chứa một số thực là thời điểm đầu tiên có một người cận vệ đặt chân tới thành phố \(k_Q\). Ghi ra \(-1\) nêu thành phố đó không có cận vệ nào đặt chân tới.
Đáp án của bạn được cho là đúng nếu sai số tuyệt đối so với đáp án của giám khảo không quá \(10^{-6}\).
Example
Test 1
Input
10 2 4
1 2 2
3 1 3
1 4 1
6 2 7
5 2 4
7 3 5
3 8 6
8 9 3
8 10 1
6 8 2 2
7 10 3 3
1 3 5 7Output
6.5
4.66666666220797
-1
3Note
Dưới đây là hình ảnh của vùng đất:\
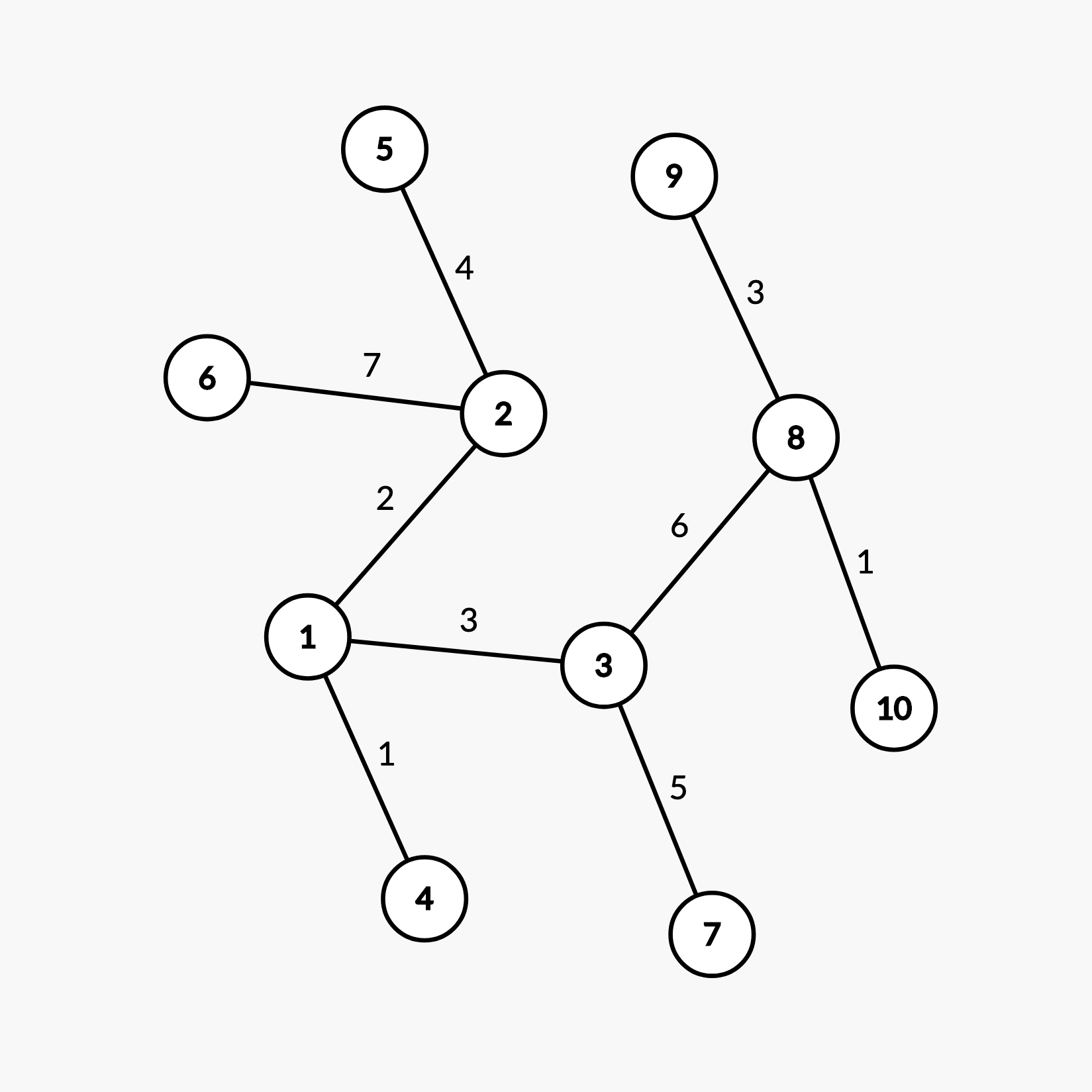
Người cận vệ thứ \(1\) đến các thành phố \([6, 2, 1, 3, 8]\) lần lượt vào các thời điểm \([2, 5\dfrac{1}{2}, 6\dfrac{1}{2}, 8, 11]\).
Người cận vệ thứ \(2\) đến các thành phố \([7, 3, 8, 10]\) lần lượt vào các thời điểm \([3, 4\dfrac{2}{3}, 6\dfrac{2}{3}, 7]\).
Các thành phố 4, 5, 9 không được ghé thăm.
Tổng kết lại, đáp án của 10 thành phố trên theo thứ tự từ 1 đến 10 là: \([6\dfrac{1}{2}, 5\dfrac{1}{2}, 4\dfrac{2}{3}, -1, -1, 2, 3, 6\dfrac{2}{3}, -1, 7]\).
Đề bài yêu cầu đáp án của 4 thành phố \(1, 3, 5, 7\) nên chúng ta in ra 4 số: \(6\dfrac{1}{2}, 4\dfrac{2}{3}, -1, 3\).
Ở dòng thứ hai của đáp án mẫu, dù đáp án không hoàn toàn đúng, nhưng số \(4.66666666220797\) có sai số tuyệt đối nằm trong mức chấp nhận được.
Constraints
- \(1 \leq N \leq 2 \times 10^{5}\)
- \(1 \leq M \leq 2 \times 10^{5}\)
- \(1 \leq Q \leq 2 \times 10^{5}\)
- \(1 \leq a_{i}, b_{i} \leq N\) \(\forall 1 \leq i \leq N\)
- \(1 \leq w_{i} \leq 10^{9}\)
- \(1 \leq u_{i}, v_{i} \leq N\), \(\forall 1 \leq i \leq M\)
- \(1 \leq t_{i}, s_{i} \leq 10^{9}\), \(\forall 1 \leq i \leq M\)
- \(1 \leq k_{i} \leq N, k_{i} \neq k_{j}\), \(\forall 1 \leq i, j \leq Q, i \neq j\)
Scoring
- Subtask \(1\) (\(20\) điểm): \(1 \leq N, M \leq 5 \times 10^{3}\).
- Subtask \(2\) (\(18\) điểm): \(a_{i} = \left \lfloor \dfrac{i + 1}{2} \right \rfloor, b_{i} = i + 1, 1 \leq i \leq N - 1\).
- Subtask \(3\) (\(16\) điểm): \(Q \le 10\).
- Subtask \(4\) (\(14\) điểm): \(s_1 = s_2 = \ldots = s_M\), \(v_{i} = 1\) \(\forall 1 \leq i \leq M\).
- Subtask \(5\) (\(12\) điểm): \(s_1 = s_2 = \ldots = s_M\).
- Subtask \(6\) (\(11\) điểm): Mỗi thành phố được kết nối trực tiếp với không quá hai con đường.
- Subtask \(7\) (\(9\) điểm): Không có ràng buộc gì thêm.
Bình luận