PVHOI3 - Bài 2: Trang trí ngày xuân
Xem PDFVậy là một mùa xuân Quý Mão lại về trên khắp muôn nơi. Xuân về là sự khởi đầu của bao chu kỳ mới: Đó là chu kỳ của một năm gồm \(12\) tháng, là chu kỳ \(4\) mùa xuân, hạ, thu, đông. Đó còn là chu kỳ sinh sôi, nảy nở của muôn loài. Xuân sang là lúc bao sức sống mới tràn về. Cỏ cây hoa lá chấm dứt thời kỳ ẩn mình cằn cỗi trong cái lạnh tái tê, chuyển sang giai đoạn xanh tươi rực rỡ. Hoà chung vào sự chuyển đổi của đất trời, con người cũng trở nên vui tươi yêu đời hơn. Mỗi dịp “năm hết, Tết đến”, chúng ta tạm gác lại những lo toan bộn bề, những thử thách khó khăn còn sót lại của năm cũ, hoà mình vào hương xuân phơi phới, tích luỹ năng lượng tràn trề và niềm tin về một năm mới ngập tràn tốt tươi. Bởi thế, cho dù cuộc sống ngày nay có gấp gáp và vội vã nhường nào, chúng ta vẫn ít nhiều chờ mong tới Tết và háo hức mỗi dịp xuân sang.
Ngày Tết quê em – Từ Huy
Ngày Tết đến trên khắp quê tôi, ngàn hoa thơm khoe sắc xinh tươi
Ngàn em thơ khoe áo mới, chạy tung tăng vui đón pháo xuân.
\(\ldots\)
Ngày Tết đến ta chúc cho nhau, một năm thêm sung túc an vui
Người nông dân thêm lúa thóc, người thương gia mau phát tài.
Mùa xuân tươi đẹp, rực rỡ, rộn rã và đầy sức sống đến thế, ấy vậy mà có người lại chỉ muốn đông ở lại mãi mà chẳng thèm xuân sang. Đó chính là Nhật Quang. Nhật Quang yêu thích mùa đông là bởi vì, Nhật Quang yêu Tuyết, và chỉ có vào mùa đông thì Tuyết mới về. Không hiểu trái tym của Nhật Quang lạnh lẽo tới đâu mà anh chàng lại có gu cô nàng dưới \(0\) độ C như vậy. Với con người ta, xuân sang là lúc tâm hồn được sưởi ấm, được thoát khỏi cái lạnh tái tê để tung tăng bay nhảy. Nhưng với Nhật Quang, thấy Tuyết tan chảy rồi dần dần biến mất, chẳng khác nào xuân sang mang ngọn lửa đốt cháy rụi con tym của chàng. Dù chán ghét xuân sang, căm thù Tết đến, nhưng thôi để giống bao người ta, Quang đành phải dọn sạch Tuyết để đặt những khóm Trúc, cành Mai trang trí khu vườn.
Khu vườn nhà Nhật Quang có dạng lưới ô vuông gồm \(r\) hàng và \(c\) cột. Các hàng được đánh số từ \(1\) đến \(r\) và các cột được đánh số từ \(1\) đến \(c\). Ô thuộc hàng \(i\) và cột \(j\) được ký hiệu là \((i, j)\). Nhật Quang dự định đặt hoa trang trí vào một số ô trong khu vườn. Vốn không muốn nhìn thấy Trúc hay Mai quá nhiều, Quang đặt ra luật sau cho việc đặt hoa trang trí: Nếu hai ô \((x_{1}, y_{1})\) và \((x_{2}, y_{2})\) thể hiện nước đi hợp lệ của quân mã trên bàn cờ, cả hai ô này không thể cùng có hoa. Nói cách khác, ít nhất một trong hai ô này phải không có hoa.
Ngoài ra, Nhật Quang còn có một dãy số đẹp \(a_{1}, a_{2}, \ldots, a_{r}\). Mỗi số trong dãy này có giá trị từ \(0\) đến \(3\). Để đặt hoa trang trí Như Ý Nhật Quang, số ô chứa hoa trên mọi hàng phải thoả mãn hai điều kiện sau:
- Nếu \(a_{i} < 3\), số ô có hoa trên hàng \(i\) phải đồng dư với \(a_{i}\) khi chia cho \(3\).
- Nếu \(a_{i} = 3\), số ô có hoa trên hàng \(i\) có thể là một giá trị bất kỳ.
Ra Tết là lúc kỳ thi học sinh giỏi quốc gia đến thật gần, Nhật Quang muốn ôn lại các bài toán đếm. Và Quang đã nghĩ ra bài toán sau: Với mỗi ô \((i, j)\) trong khu vườn, có bao nhiêu cách đặt hoa trang trí mà Nhật Quang cho là Như Ý, đồng thời ô \((i, j)\) có được đặt hoa?
Nhắc lại, hai ô \((x_{1}, y_{1})\) và \((x_{2}, y_{2})\) thể hiện nước đi hợp lệ của quân mã trên bàn cờ khi và chỉ khi \((x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2} = 5\). Hai cách đặt hoa trang trí được coi là khác nhau khi và chỉ khi tồn tại một ô có hoa ở cách này, nhưng lại không có hoa ở cách khác.
Input
- Dòng đầu tiên chứa hai số nguyên \(r\) và \(c\) \((1 \leq r \leq 60,1 \leq c \leq 10)\).
- Dòng thứ hai chứa \(r\) số nguyên \(a_{1}, a_{2}, \ldots, a_{r}\) \((0 \leq a_{i} \leq 3)\).
Output
- Gồm \(r\) dòng, mỗi dòng chứa \(c\) số nguyên. Số thứ \(j\) trên dòng thứ \(i\) là số cách đặt hoa trang trí Như Ý Nhật Quang mà ở đó ô \((i, j)\) có hoa. Do kết quả có thể rất lớn, các bạn chỉ cần in phần dư của các số này khi chia cho \(10^{9} + 19972207\).
Scoring
- Subtask \(1\) (\(14\) điểm): \(r \cdot c \leq 21\)
- Subtask \(2\) (\(8.4\) điểm): \(c = 1\)
- Subtask \(3\) (\(8.4\) điểm): \(c = 2\)
- Subtask \(4\) (\(11.2\) điểm): \(c \leq 4\)
- Subtask \(5\) (\(12.6\) điểm): \(c \leq 6\)
- Subtask \(6\) (\(15.4\) điểm): Không có ràng buộc gì thêm.
Example
Test 1
Input
3 3
1 0 3Output
4 4 4
2 2 2
4 2 4Note
Trong ví dụ trên, khu vườn nhà Nhật Quang có dạng lưới ô vuông gồm \(3\) hàng và \(3\) cột.
- Do \(a_{1} = 1\) nên số ô có hoa trên hàng \(1\) phải chia \(3\) dư \(1\) (tức phải bằng \(1\)).
- Do \(a_{2} = 0\) nên số ô có hoa trên hàng \(2\) phải chia \(3\) dư \(0\) (tức bằng \(0\) hoặc \(3\)).
- Do \(a_{3} = 3\) nên số ô có hoa trên hàng \(3\) có thể là một giá trị bất kỳ.
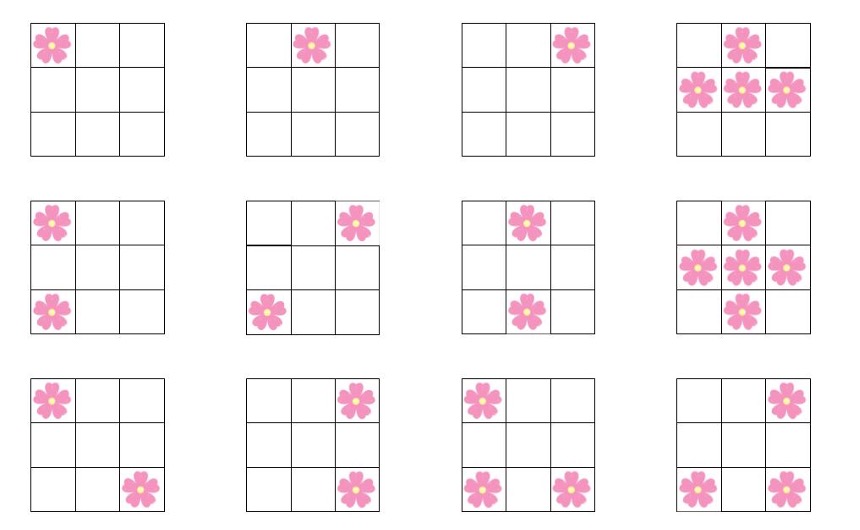
Hình vẽ dưới đây thể hiện tất cả \(12\) cách đặt hoa trang trí mà Nhật Quang cho là Như Ý.
Bình luận