Có một lưới ô vuông có kích thước \(N × N\) được đánh chỉ số hàng từ \(1\) đến \(N\) (theo chiều từ trên xuống dưới) và chỉ số cột từ \(1\) đến \(N\) (theo chiều từ trái sang phải). Mỗi ô trong lưới được xác định vị trí bởi một cặp số \((i; j)\) trong đó \(i\) là chỉ số hàng và \(j\) là chỉ số cột.

Tại ô \((1; 1)\) người ta đặt một con robot tự hành. Mỗi lần di chuyển robot chỉ đi sang phải một ô hoặc đi xuống dưới một ô. Trong lưới ô vuông này người ta đặt một viên đá vào một số ô để làm vật cản.

Yêu cầu: Hãy tính xem có bao nhiêu đường đi từ ô \((1; 1)\) đến ô \((N; N)\). Biết rằng robot không thể đi vào ô có vật cản và hai đường đi được gọi là khác nhau nếu có ít nhất một ô thuộc đường đi này nhưng không thuộc đường đi kia.

VD: Xét lưới ô vuông kích thước \(3\times 3\) như hình vẽ sau:

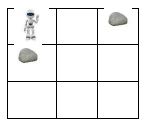
Trong lưới ô vuông \(3\times 3\) này người ta đặt viên đá vào ô \((1;3)\) và ô \((2;1)\).
Với dữ kiện trên thì robot có tất cả 2 đường đi như sau:

\((1;1) → (1;2) → (2;2) → (2;3) → (3;3)\)

\((1;1) → (1;2) → (2;2) → (3;2) → (3;3)\)

Input

Đọc từ file văn bản ROBOT.INP có cấu trúc như sau:

• Dòng đầu tiên chứa 2 số nguyên dương \(N\) và \(M\) (mỗi số cách nhau 1 dấu cách; \(M < N\)).
• \(M\) dòng tiếp theo, mỗi dòng ghi 2 số nguyên dương \(i\) và \(j\) (mỗi số cách nhau một dấu cách) là chỉ số hàng và chỉ số cột của ô được đặt vào đó một viên đá là vật cản.

Output

• Ghi ra file văn bản ROBOT.OUT một số \(k\) là số đường đi của robot từ ô \((1; 1)\) đến ô \((N; N)\).

Scoring

• Subtask \(1\) (\(30\%\) số điểm): \(N \le 10\).
• Subtask \(2\) (\(40\%\) số điểm): \(10 < N \le 30\).
• Subtask \(3\) (\(30\%\) số điểm): \(30 < N \le 100\).

Example

3 2
1 3
2 1

2