Những chuyến bay
Xem PDFVào kỷ nguyên mới, thế giới chia thành \(n\) quốc gia, tạm đánh số từ \(1\) tới \(n\). Lúc này, Phong đang ở quốc gia \(1\), và Hải đang nghỉ hưu tại quốc gia \(n\) và Phong lên kế hoạch đi thăm Hải.
Thời kỳ này mỗi quốc gia chỉ có một sân bay đặt tại thủ đô. Phong có \(k\) phiếu voucher của hãng hàng không VA. Hãng VA có \(m\) đường bay được đánh số từ \(1\) đến \(m\), đường bay thứ \(i\) đi từ thủ đô của quốc gia \(u_i\) tới thủ đô của quốc gia \(v_i\), có giá vé là \(w_i\). Tuy nhiên, nếu Phong đặt vé cho đường bay thứ \(i\) và áp dụng voucher, thì giá vé được áp dụng là \(-w_i\). Vì thế, Phong hoàn toàn có thể gặp Hải mà không hề mất đồng nào, thậm chí là được thêm tiền.
Lưu ý:
- Có đường bay đi từ quốc gia \(u\) đến quốc gia \(v\) không có nghĩa là sẽ có đường bay đi từ quốc gia \(v\) đến quốc gia \(u\).
- Một đường bay có thể được đi qua nhiều lần, và mỗi lần di chuyển đều phải mua một vé riêng.
- Mỗi phiếu voucher chỉ có hiệu lực trong \(1\) lần di chuyển, áp dụng lên duy nhất một vé.
Phong tìm cách đặt vé của một số chuyến bay, để di chuyển từ thủ đô của quốc gia \(1\) tới thủ đô của quốc gia \(n\), sao cho số tiền phải bỏ ra là ít nhất. Nói cách khác, giả sử Phong đặt \(k\) chuyến bay thứ \(f_1, f_2, \dots, f_k\) \((k \geq 1)\), với chuyến bay thứ \(i\) mua vé của đường bay \(f_i\) và giá vé sau khi áp dụng voucher (hoặc không) là \(w'_i\) (\(w'_i = w_i\) nếu Phong không sử dụng voucher, hoặc \(w'_i = -w_i\) nếu Phong sử dụng voucher); thì \(v_{f_i} = u_{f_{i+1}} \ (\forall 1 \le i < k)\), \(u_{f_1} = 1\), \(v_{f_k} = n\) và tổng \(w'_1 + w'_2 + \dots + w'_k\) phải là \textbf{nhỏ nhất có thể}.
Yêu cầu: Hãy tìm cách đặt vé giúp Phong để anh ta sớm được gặp Hải!
Input
- Dòng đầu tiên lần lượt chứa ba số nguyên dương \(n, m, k\) \((1 \le n \le 10^5; 1 \le m \le 2 \times 10^5; 0 \le k \le 100)\).
- \(m\) dòng sau, dòng thứ \(i\) chứa ba số \(u_i, v_i, w_i\) \((1 \le u_i, v_i \le n; u_i \neq v_i; 1 \le w_i \le 10^9)\).
Output
- In ra một số nguyên duy nhất là kết quả của bài toán. Dữ liệu vào đảm bảo luôn có cách đi từ thủ đô của quốc gia \(1\) tới thủ đô của quốc gia \(n\) bằng một hoặc nhiều tuyến bay.
Scoring
- Subtask \(1\) (\(15\) điểm): \(k = 0\)
- Subtask \(2\) (\(21\) điểm): \(k = 1\)
- Subtask \(3\) (\(23\) điểm): \(e^{u_i} - e^{v_i} < u_i - v_i\) với mọi \(1 \leq i \leq m\).
- Subtask \(4\) (\(22\) điểm): \(n \le 1000; m \le 3000\)
- Subtask \(5\) (\(19\) điểm): Không có ràng buộc gì thêm.
Example
Test 1
Input
7 10 1
1 2 2
1 5 1
2 3 1
3 6 1
4 3 2
4 7 2
5 4 3
6 4 4
6 7 3
4 1 2Output
0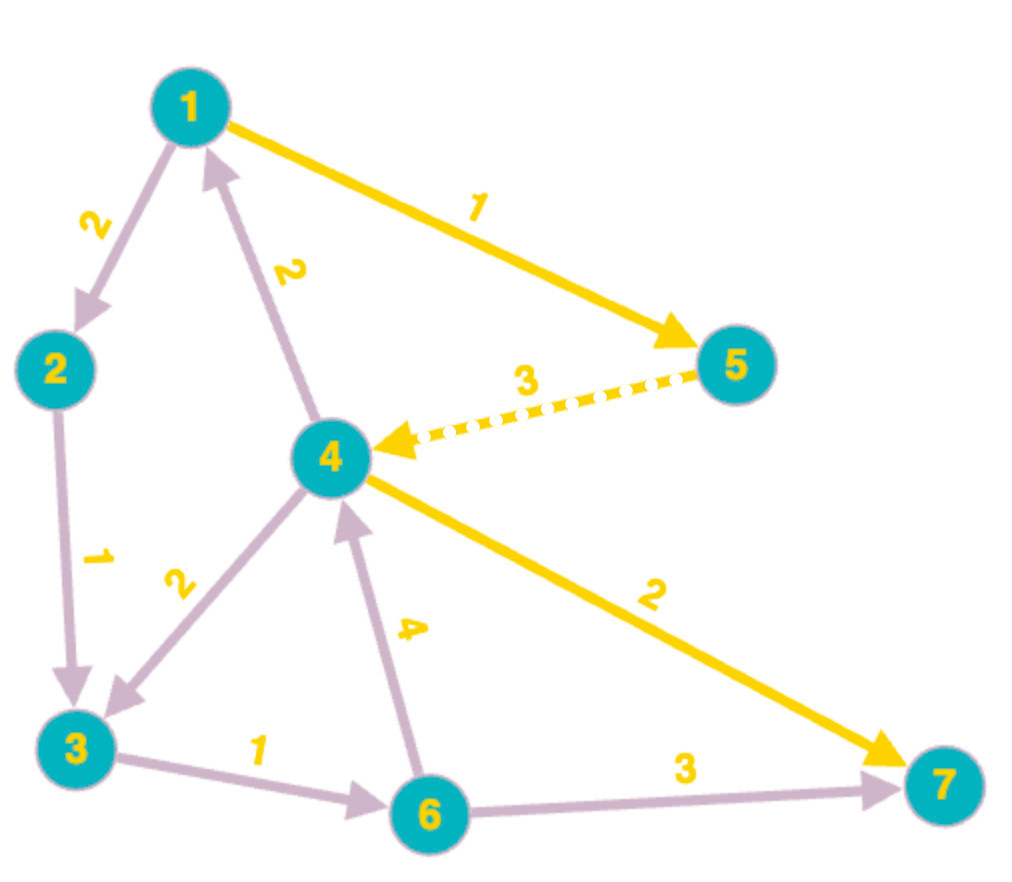
Bình luận