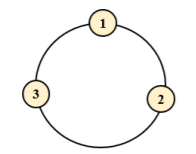
Nhảy lò cò là trò chơi dân gian của Việt Nam. Thuở bé Lan rất thích trò chơi này. Vì vậy, khi được học môn “Thiết kế và phân tích thuật toán”, Lan đã đặt ra bài toán khá thú vị liên quan đến một dạng của trò chơi này. Trên mặt phẳng vẽ \(N\) vòng tròn. Các vòng tròn này lại được xếp trên một vòng tròn lớn và được đánh số từ 1 đến \(N\) theo chiều đi vòng quanh vòng tròn lớn thuận chiều kim đồng hồ (xem minh họa ở hình 1 với \(N=3\)). Hai vòng tròn nhỏ liên tiếp nhau theo một chiều đi vòng quanh vòng tròn lớn được gọi là ở bên cạnh nhau.

Trò chơi lò cò trên vòng tròn (\(N=3\))

Người chơi bắt đầu từ vòng tròn đánh số 1, mỗi bước nhảy người chơi sẽ di chuyển sang một trong hai vòng tròn bên cạnh. Bài toán mà Lan cần giải quyết là: Đếm xem có bao nhiêu cách khác nhau thực hiện \(K\) bước nhảy bắt đầu từ vòng tròn 1 rồi lại quay về vòng tròn 1.

Yêu cầu: Giúp Lan giải quyết bài toán đặt ra.

Input

• Gồm duy nhất một dòng chứa ba số nguyên dương \(N, K, M\ (N \le 4000; M \le 10^9+7\)) được ghi cách nhau bởi dấu cách theo thứ tự là số lượng vòng tròn và số lượng bước nhảy.

Output

• Gồm một số nguyên là phần dư trong phép chia số lượng cách nhảy tìm được cho \(M\)

Scoring

• Subtask \(1\) (\(10\%\) số điểm): \(K \le 20\).
• Subtask \(2\) (\(30\%\) số điểm): \(K \le 10^4\).
• Subtask \(3\) (\(60\%\) số điểm): \(K \le 10^6\).

Example

3 4 100

6

1, 2, 3, 2, 1;
1, 3, 2, 3, 1;
1, 2, 1, 2, 1;
1, 3, 1, 3, 1;
1, 2, 1, 3, 1;
1, 3, 1, 2, 1.