Hướng dẫn cho LQDOJ Contest #6 - Bài 2 - Đường Đi Ngắn Nhất
Chép code từ bài hướng dẫn để nộp bài là hành vi có thể dẫn đến khóa tài khoản.
Authors:
Subtask 1
Subtask này các bạn sinh trâu tất cả các trường hợp bằng BFS, đếm phân phối số lượng cách đi, xin phép không trình bày thuật này do quá đơn giản.
Subtask 2
Dễ dàng nhận ra ngay đoạn đường ngắn nhất từ ô \(\left(1,\ 1\right)\rightarrow(i,\ j)\) có độ dài là \(i+j-1\).
Gọi \(f(m,\ n)\) là số cách đi có độ dài \(m+n-1\), có ngay công thức truy hồi:
\(f\left(m,\ n\right)=f\left(m-1,\ n\right)+f(m,\ n-1)\). Do \(i\le 1000\) và \(j\le1000\) nên các bạn có thể tạo mảng hai chiều cho công cuộc tính đáp án.
Subtask 3
Subtask này tương tự Subtask 2 nhưng yêu cầi các bạn có xử lí tối ưu mảng \(f\) hai chiều ban đầu một chút.
Ta có \(2\) cách để tối ưu như sau:
- Cách \(1\): Các bạn thay vì viết \(f[i][j]\), có thể thay bằng \(f[\left(i-1\right)\times n+j]\), tức là đưa mảng \(f\) về mảng một chiều.
- Cách \(2\): Các bạn thay vì viết \(f[i][j]\), có thể viết \(f[i \ mod\ 2][j]\) vì rõ ràng, trong công thức, \(f\left[i\right]\left[j\right]\) chỉ được tổng hợp từ dòng trên nó và cùng dòng \(i\), từ đó qui hàm mục tiêu về mảng \(2\) chiều \(f[0..1][1..10^7]\)
Subtask 4,5
Hai Subtask cuối này là mục tiêu chính của bài này, nhằm giúp các bạn phát huy khả năng làm toán của mình.
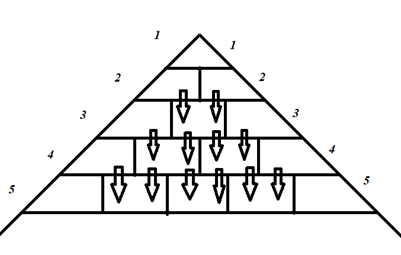
Ta xét phép xoay mảng \(f[][] 45^\circ\):
Dễ dàng nhận ra ngay ô thứ \((i,\ j)\) được tổng hợp từ \(2\) ô trên đầu nó, và ai cũng biết rằng đó là cách tạo ra tam giác Pascal, khai triển nhị thức Newton cực kì phổ biến. Tức là bài toán qui về tính một ô trong tam giác Pascal. Vậy làm sao để tính ô thứ \(\left(i,\ j\right)\) bằng nhận xét trên?
Đầu tiên, ta dễ dàng nhận thấy, nếu trong mảng \(f\), ô đó là \((i,\ j)\) thì trong tam giác Pascal, ô đó sẽ là \((i+j-1,\ j)\). Tiếp theo, ta sẽ bàn về cách tính ô \(\left(i+j-1,\ \ j\right)\) trong tam giác Pascal.
Như ta đã học về tổ hợp, ô này có giá trị là \(C_{j-1}^{i+j-2}\) với \(C_j^i\) là tổ hợp chập \(i\) của \(j\) và cũng chính là đáp án của bài toán.
Đến đây thì các bạn đã có thể code được rồi, và khúc các bạn code là lí do đề có thêm subtask 5, yêu cầu các bạn phải code tối ưu hơn. Chúc các bạn may mắn :Đ
Nếu các bạn vẫn chưa biết code ra sao thì hãy kéo xuống và đọc tiếp cách giải quyết của người ra đề - .
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
\(.\)
Ta có \(C_{j-1}^{i+j-2}=\frac{\left(i+j-2\right)!}{(j-1)!(i-1)!}\)
Vấn đề là ta phải tính theo dạng \(\frac{a}{b}\ mod\ c\) mà phép chia thì chẳng có định lý gì cho nó về đồng dư cả.
Nhưng nhận ra ngay là do \(c\) là số nguyên tố (đề cho) nên theo định lý Fermat nhỏ thì:
\(b^c\equiv b\ \left(mod\ c\right)\)
\(b^{c-2}\equiv\frac{1}{b}(mod\ c)\)
\(\frac{a}{b}\equiv ab^{c-2}\ (mod\ c)\)
Vậy việc cần làm là tính \((i+j-2)! \times ((i-1)!(j-1)!)^{10^9+5}\) \(mod\) \(10^9+7\).
Đến đây phần việc của các bạn là tính cái mũ to to kia kìa, đến đây thì việc tính là của các bạn. Mình sẽ gợi ý rằng có thể dùng chia để trị để giải quyết nó :Đ
Bình luận (2)