Rùa Và Câu Chuyện Xây Cầu
Xem PDFBạch Tuộc là con vật có tập tính sống đơn lẻ, vì vậy nó rất cô đơn. Rùa thấy vậy nên thường rủ Bạch Tuộc sang chơi. Tuy nhiên Bạch Tuộc lần nào cũng đến muộn, làm cho buổi gặp mặt không còn vui vẻ nữa. Vấn đề ở đây là, nếu muốn tới nhà Rùa chơi, Bạch Tuộc phải băng qua \(1\) con sông. Rùa thấy vậy nên quyết tâm giúp Bạch Tuộc một phen.
Dòng sông là một ma trận gồm \(n\) hàng và \(m\) cột. Ở cột \(i\) hàng \(j\) chứa một số nguyên là \(a_{i,j}\) là độ sâu của con sông tại vị trí tương ứng. Cột đầu tiên và cuối cùng là hai phía bờ của dòng sông, vì vậy độ sâu sẽ là \(0\).
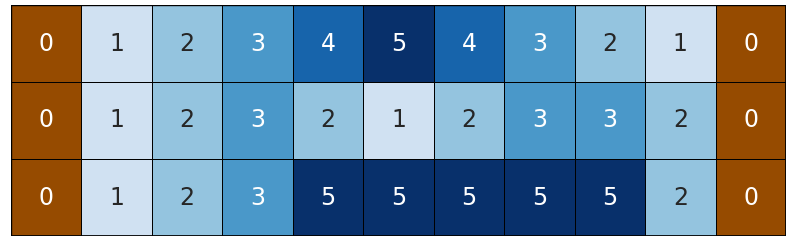
Rùa có thể chọn hàng thứ \(i\), là các ô \((i, 1), (i, 2), ..., (i, m)\), và xây một cây cầu ngang qua hàng đó. Ở một ô bất kì của hàng, Rùa có thể xây dựng một cọc đỡ cho cầu. Để xây một cọc đỡ ở ô \((i, j)\) thì Rùa sẽ mất chi phí là \(a_{i,j} + 1\). Tuy nhiên, vì hạn chế của vật liệu xây dựng, các cọc đỡ phải thỏa mãn các điều kiện sau:
- Cọc đỡ phải được xây dựng ở ô \((i, 1)\) và \((i, m)\) (hai bên bờ của dòng sông)
- Khoảng các giữa \(2\) cọc đỡ bất kì phải nhỏ hơn \(d\). Có nghĩa là cọc đỡ ở ô \((i, j_{1})\) và \((i, j_{2})\) phải có \(|j_{1} - j_{2}| - 1 \leq d\)
Vì xây nếu chỉ xây một cây cầu thì quá nhỏ, không ứng dụng được nhiều. Vì vậy Rùa quyết định xây \(k\) cây cầu liên tiếp. Có nghĩa là Rùa sẽ chọn một hàng \(i\) với \(1 \leq i \leq n - k + 1\), sau đó xây \(k\) cây cầu ở các hàng \(i, i + 1, ..., i - k + 1\).
Để tính được bằng cơm lượng chi phí ít nhất để xây dựng \(k\) cây cầu cần rất nhiều thời gian và công sức. Vì vậy hãy viết chương trình tính giúp Rùa cách thức xây cầu thế nào để tốn ít chi phí nhất.
Dữ liệu:
- Dòng 1 gồm các số nguyên dương \(n, m, k, d\) \((1 \leq k \leq n \leq 100, 3 \leq m \leq 10^4, 1 \leq d \leq m)\)
- \(n\) dòng tiếp theo, dòng thứ \(i\) chứa \(m\) số nguyên dương \(a_{i,j}\) \((1 \leq j \leq m, 0 \leq a_{i,j} \leq 10^6, a_{i,1} = a_{i, m} = 0)\)
Kết quả
- Gồm một dòng duy nhất chứa một số nguyên dương là kết quả bài toán
Example
Test 1
Input
3 11 1 4
0 1 2 3 4 5 4 3 2 1 0
0 1 2 3 2 1 2 3 3 2 0
0 1 2 3 5 5 5 5 5 2 0 Output
4Test 1
Input
4 5 2 5
0 1 1 1 0
0 2 2 2 0
0 2 1 1 0
0 3 2 1 0Output
4Note
Các cọc cầu có thể được đặt trên 2 bên bờ sông, chọn xây 2 cây cầu ở vị trí bất kì đều cần tổng chi phí là 4
Bình luận
hài sao mà hài, sinh test sai cũng up đề cho được
2 bình luận nữa