PVHOI3 - Bài 3: Đếm chu trình
Xem PDFLý thuyết đồ thị là một mảng kiến thức vô cùng lớn và quan trọng bậc nhất của Toán rời rạc cũng như Lập trình thi đấu. Chính bởi vậy, đề thi học sinh giỏi quốc gia năm nào cũng chứa từ một tới hai bài toán đồ thị. Để chuẩn bị tốt nhất cho kỳ thi lớn sắp tới, hãy cùng nhau ôn lại đồ thị thông qua bài tập này nhé!
Trong bài tập này, ta chỉ xét các đồ thị vô hướng không chứa khuyên (cạnh nối một đỉnh với chính nó). Nói cách khác, đồ thị trong bài tập này có thể chứa cạnh lặp (tức giữa hai đỉnh có thể có nhiều cạnh nối), nhưng mỗi cạnh luôn nối hai đỉnh khác nhau.
Dưới đây là hình ảnh của một đồ thị vô hướng gồm \(13\) đỉnh và \(16\) cạnh:
Giờ ta xét tới khái niệm chu trình đơn. Một chu trình đơn trong đồ thị vô hướng là một tập hợp con khác rỗng \(S\) của tập hợp các cạnh trên đồ thị thoả mãn các tính chất dưới đây:
- Mọi đỉnh trên đồ thị kề với \(0\) hoặc \(2\) cạnh trong \(S\).
- Các cạnh trong \(S\) liên thông với nhau. Nói cách khác, với mọi cặp đỉnh \((u, v)\) của đồ thị sao cho cả \(u\) và \(v\) đều kề với ít nhất một cạnh thuộc \(S\), luôn tồn tại đường đi giữa \(u\) và \(v\) chỉ đi qua các cạnh thuộc \(S\).
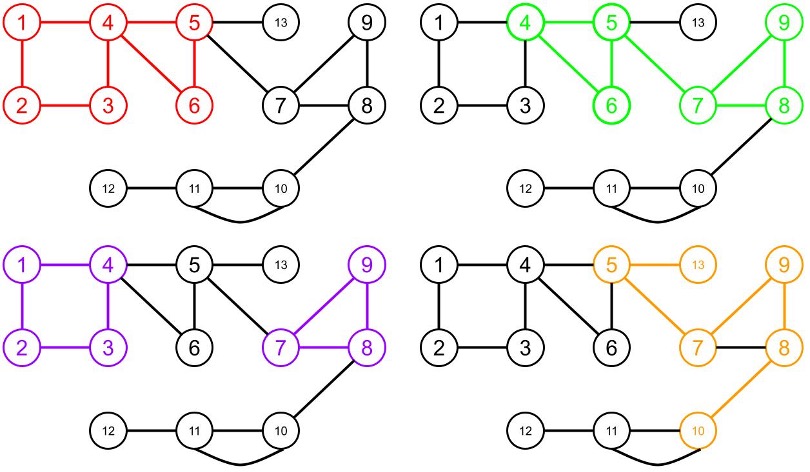
Hình dưới đây thể hiện các chu trình đơn của đồ thị trên:
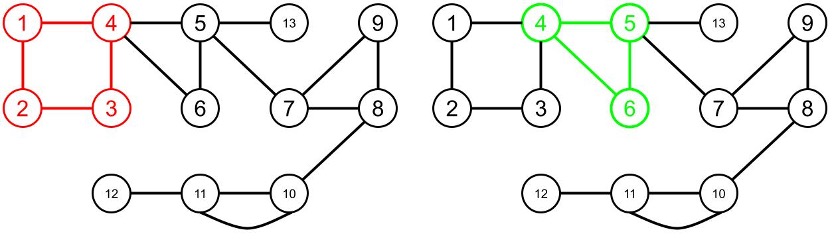
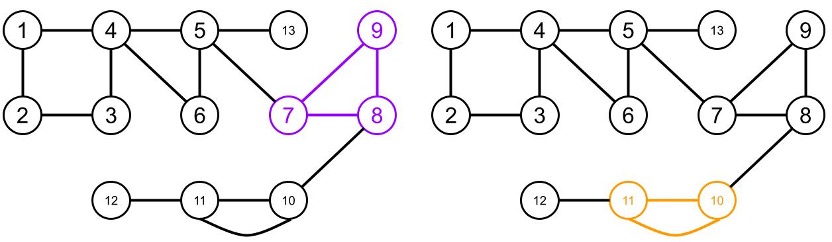
Hình dưới đây thể hiện một số tập hợp cạnh không thoả mãn các tính chất của chu trình đơn vì:
- Trong tập cạnh màu đỏ (hình góc trên bên trái), đỉnh \(4\) kề với \(4\) cạnh trong tập.
- Trong tập cạnh màu xanh (hình góc trên bên phải), đỉnh \(5\) kề với \(3\) cạnh trong tập.
- Tập cạnh màu tím (hình góc dưới bên trái) không thoả mãn điều kiện liên thông.
- Trong tập cạnh màu cam (hình góc dưới bên phải), đỉnh \(10\) kề với \(1\) cạnh trong tập.
Cây là một đồ thị vô hướng liên thông và không có chu trình. Một cây gồm \(n\) đỉnh luôn có chính xác \(n - 1\) cạnh.
Trong bài tập này, bạn được cho một cây gồm \(n\) đỉnh. Các đỉnh được đánh số từ \(1\) đến \(n\), các cạnh được đánh số từ \(1\) đến \(n - 1\). Cạnh thứ \(i\) nối hai đỉnh \(x_{i}\) và \(y_{i}\). Bạn cần trả lời \(q\) câu hỏi. Trong mỗi câu hỏi, bạn được cho sáu số nguyên \(e_{1}, u_{1}, v_{1}, e_{2}, u_{2}, v_{2}\) thoả mãn \(1 \leq e_{1}, e_{2} < n, 1 \leq u_{1}, v_{1}, u_{2}, v_{2} \leq n, e_{1} \neq e_{2}, u_{1} \neq v_{1}\) và \(u_{2} \neq v_{2}\). Bạn cần xây dựng một đồ thị mới bằng cách lấy cây ban đầu, xoá đi hai cạnh \(e_{1}\) và \(e_{2}\) đồng thời thêm hai cạnh \((u_{1}, v_{1})\) và \((u_{2}, v_{2})\), sau đó đếm số chu trình đơn trong đồ thị mới này. Chú ý rằng, cây ban đầu không bị biến đổi trong suốt các câu hỏi. Đồ thị trong mỗi câu hỏi đều được xây dựng từ cây ban đầu, với hai cạnh bị xoá đi và hai cạnh được thêm mới.
Để giảm kích thước file dữ liệu và file kết quả, thay vì cho trực tiếp các tham số và yêu cầu in kết quả của mọi câu hỏi, bạn cần xét đoạn mã nguồn sau:
const int MOD = (int)1e9 + 19972207;
int cur = seed;
int getRandom(int n) {
cur = (1LL * mul * cur + add) % MOD;
return 1 + cur % n;
}
int gspvhcute(void) {
int res = 0;
for (int i = 1; i <= q; i++) {
int e1 = getRandom(n - 1);
int u1 = getRandom(n); int v1 = getRandom(n);
int e2 = getRandom(n - 1);
int u2 = getRandom(n); int v2 = getRandom(n);
int tmp = e1 == e2 || u1 == v1 || u2 == v2
? MOD - 1 : query(e1, u1, v1, e2, u2, v2);
res = (227LL * res + tmp) % MOD;
}
return res;
}
Trong đoạn mã nguồn trên, hàm query(e1, u1, v1, e2, u2, v2) nhận vào sáu tham số và trả về một số nguyên, là số chu trình đơn trong câu hỏi với các tham số \(e_{1}, u_{1}, v_{1}, e_{2}, u_{2}, v_{2}\) theo định nghĩa ở trên. Bạn được cho biết giá trị của các biến seed, mul, add trong đoạn mã nguồn ở trên; hãy xác định kết quả trả về của hàm gspvhcute.
Vui lòng xem kỹ phần giải thích để hiểu rõ hơn về đoạn mã nguồn này.
Input
- Dòng đầu tiên chứa số nguyên \(\theta\) \((1 \leq \theta \leq 6)\) là số thứ tự của subtask chứa test này.
- Dòng thứ hai chứa số nguyên \(n\) \((2 \leq n \leq 150000)\).
- Trong \(n - 1\) dòng tiếp theo, dòng thứ \(i\) chứa hai số nguyên \(x_{i}\) và \(y_{i}\) \((1 \leq x_{i}, y_{i} \leq n)\) mô tả cạnh thứ \(i\) của cây ban đầu. Dữ liệu vào đảm bảo \(n - 1\) cạnh này tạo thành cây.
- Dòng cuối cùng chứa bốn số nguyên \(q, seed, mul, add\) \((1 \leq q \leq 5555555,1 \leq seed, mul, add \leq 10^{9})\) lần lượt là số câu hỏi và giá trị của các biến trong đoạn mã nguồn ở trên.
Output
- In ra một số nguyên duy nhất là kết quả trả về của hàm
gspvhcute.
Scoring
- Subtask \(1\) (\(12\) điểm): \(n \leq 16\) và \(q \leq 89\)
- Subtask \(2\) (\(12\) điểm): Trong cây ban đầu, mỗi đỉnh kề với ít hơn ba đỉnh khác.
- Subtask \(3\) (\(7.2\) điểm): \(n \leq 50\) và \(q \leq 7000\)
- Subtask \(4\) (\(7.2\) điểm): \(n \leq 3000\) và \(q \leq 40000\)
- Subtask \(5\) (\(9.6\) điểm): \(q \leq 200000\)
- Subtask \(6\) (\(12\) điểm): Không có ràng buộc gì thêm.
Example
Test 1
Input
1
10
1 4
8 9
7 9
3 4
3 9
2 9
3 10
1 5
1 6
3 22 7 1997Output
51528Note
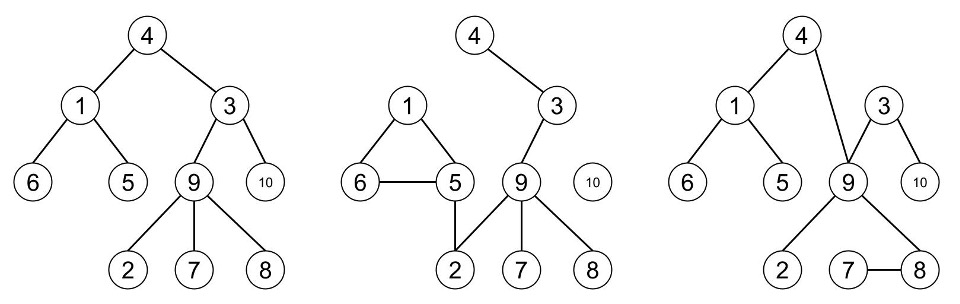
Trong ví dụ trên, \(q = 3\). Vòng lặp for trong đoạn mã nguồn trên diễn ra như sau:
- Tại \(i = 1\), ta có \((e_{1}, u_{1}, v_{1}, e_{2}, u_{2}, v_{2}) = (1, 5, 6, 7, 2, 5)\). Hàm
queryđược gọi và trả về \(1\). Do đó giá trị biếnrestrở thành \((227 \cdot 0 + 1) \% MOD = 1\). - Tại \(i = 2\), ta có \((e_{1}, u_{1}, v_{1}, e_{2}, u_{2}, v_{2}) = (4, 9, 4, 3, 7, 8)\). Hàm
queryđược gọi và trả về \(0\). Do đó giá trị biếnrestrở thành \((227 \cdot 1 + 0) \% MOD = 227\). - Tại \(i = 3\), ta có \((e_{1}, u_{1}, v_{1}, e_{2}, u_{2}, v_{2}) = (5, 4, 4, 4, 7, 3)\). Do \(u_{1} = v_{1}\) nên giá trị biến tmp là \(MOD - 1\). Giá trị biến
reslúc này là \((227 \cdot 227 + MOD - 1) \% MOD = 51528\).
Trong hình vẽ dưới đây, từ trái qua phải lần lượt là cây lúc ban đầu, đồ thị được xét bởi hàm query khi \(i = 1\) và khi \(i = 2\).
Bình luận
SOS
2 bình luận nữa