Giải 2 dấu sigma

Xem PDF
Tất cả bài nộp
Các bài nộp tốt nhất
Tác giả:
Toilaaibanbietko7A4
Dạng bài
Điểm: 350 (p) Thời gian: 1.0s Bộ nhớ: 1G Input: bàn phím Output: màn hình

Từ sau cái hôm làm bánh cho ông nguyenminhhai021009 ấy (xem lại bài Bán Bánh Dày), dù tôi kiếm được nhiều tiền nhưng lại bị mất kha khá khách (do bữa đó chỉ lo làm bánh cho ổng thôi mà). Mấy hôm sau, tôi có nhận được tin nhắn của ổng: "Hãy đến địa chỉ này gặp tôi" cùng với địa chỉ lạ. Tôi tới nơi thì, chao ôi, đó là một công ty lớn chuyên về ngành Toán học tên Mathtics. Tôi thấy ông Hải đứng ngoài cửa công ty rôi vẫy tay gọi tôi vào. Hóa ra, ông là Phó Giám Đốc của công ty này, vì nghe đồn tôi là người rất giỏi Toán nên tới thử tài. Vì tôi đã thỏa mãn được yêu cầu của ông lúc đó nên được gọi đến để phỏng vấn vào chức vụ Trợ lí của ngài Giám Đốc Công Ty stack_queue_4977. Tôi được đưa vào phòng của ngài, ngồi xuống ghế trước mặt ngài ấy. Ngài ấy bảo rằng ông rất ấn tượng về việc tôi hoàn thành thử thách của vị Phó Giám Đốc kia, và bảo nếu tôi trả lời chính xác \(Q\) câu hỏi toán mà ông sắp đưa cho tôi đây, thì ông sẽ tuyển dụng tôi ngay, khỏi bàn cãi. Tôi nhận đề, trên đề ghi như sau:

"Cho \(Q\) truy vấn, mỗi truy vấn gồm 2 số \(n\) và \(k\). Tính \(P^k_n\) \(\text{mod}\) \(10^{18}\) biết:"

"Ôi trời ơi khó quá!!!" - Tôi than ở trong đầu. Tôi chưa từng thấy bài thi nào khó như vậy. Tôi đang khổ sở thì nhớ ra các bạn coder LQDOJ. Các bạn ơi, các bạn hãy giải giúp tôi bài thi này để tôi được tuyển dụng nhé. Cảm ơn các bạn rất nhiều!!!!

Input

  • Dòng 1 gồm số \(Q\).

  • \(Q\) dòng tiếp theo, mỗi dòng gồm 2 số \(n\) và \(k\).

Output

  • Với mỗi truy vấn, in ra \(P^k_n\) \(\text{mod}\) \(10^{18}\).

Scoring

  • Subtask \(1\) (\(40\%\) số điểm): \(1\le Q \le 50000\).

  • Subtask \(2\) (\(100\%\) số điểm): \(1 \le Q \le 150000\).

  • Trong mỗi test:

    • 30% số test_case có \(1 \le n,k \le 10^5\).

    • 100% số test_case có \(1 \le n,k \le 10^{18}\).

Example

Test 1

Input 
1
1 1
Output 
1

Note

Bài này đọc xong thấy có dễ ko mn :))

Phần giải thích cho mấy bạn chưa hiểu đề lắm:

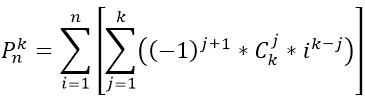
  • Dấu Sigma (hai dấu ở đầu biểu thức sau dấu = là dấu Sigma) là kí hiệu lấy tổng. Xem link này để hiểu rõ hơn.

  • Kí hiệu \(C^j_k\) bạn thấy là kí hiệu toán học của tổ hợp. Xem link này để hiểu rõ hơn.

Bình luận


  • 5
    nguyendanghau2006    11:35 p.m. 28 Tháng 1, 2022 ← chỉnh sửa 3

    || hint
    sau 2 năm, tui cũng đã tìm ra công thức của bài này, sau đây mình sẽ chia sẽ công thức với mọi người mặc dù mình chưa ac(mình yếu phần modulo quá í mà :D). công thức của bài này là n ^ k (n mũ k). mình tìm được công thức này nhờ vào nhị thức niu-tơn, mọi người có thể tham khảo nhị thức niu-tơn tại đây https://toanthaydinh.com/nhi-thuc-newton/. chúc mọi người ac cho Toilaaibanbietko7A4 vui nha :D.
    ||


    • 2
      huyhau6a2    10:22 a.m. 29 Tháng 1, 2022

      Thực chất ta chỉ cần test các th n, k nhỏ là ra công thức thôi, chứ mình chả biết nhị thức niuton là gì hết á


    • 3
      VoBaThongL921    9:49 a.m. 29 Tháng 1, 2022

      ui công thức hay phết :)) còn về module thì ông xài __int128, dùng công thức mod lũy thừa như bình thường và dùng lũy thừa nhị phân là đc á 😃


      • 2
        minhtuanitk20    7:04 p.m. 29 Tháng 1, 2022

        luỹ thừa nhị phân bậc cao


        • 2
          nguyendanghau2006    9:59 a.m. 29 Tháng 1, 2022 ← đã chỉnh sửa

          Tui chịu á :)), dùng __int128 cũng ko được


        • 3
          Toilaaibanbietko7A4    6:02 a.m. 29 Tháng 1, 2022 ← đã chỉnh sửa

          Yê cảm ơn bạn đã cung cấp hint cho bài này :)) chính xác đấy. Nhưng vấn đề là \(n, k\) vẫn quá lớn, cần hiểu rõ về modulo mới AC đc nhoa

        9 bình luận nữa